/* personal notes of renzo diomedi */
~ 00001101 ~
Shift Instructions
Multiplying and dividing are two of the most time-consuming operations on the processor. However,
there are some tricks that you can use to help speed things up. The shift instructions provide a quick and
easy way to perform multiplication and division based on powers of 2. This section describes the methods
used to perform multiplication and division using the shift instructions.
Shifting utilizes a feature of binary arithmetic that makes multiplying and dividing by powers of 2 simple.
You are probably familiar with the decimal world, and how shifting a decimal value into another
decimal place automatically multiplies or divides it by a power of 10 (for example, moving the value
2 over one decimal place to 20 is the same as multiplying it by 10).
The same principle applies to binary numbers, except using powers of 2. Shifting a binary number to the
left one space multiplies it by 2, two spaces multiplies it by 4, three spaces multiplies it by 8, and so on.
Shifting bits in a data element is much quicker than performing binary multiplication and can be used to
increase the performance of mathematically intensive programs.
Multiply by shifting
To multiply integers by a power of 2, you must shift the value to the left. Two instructions can be used to
left shift integer values, SAL (shift arithmetic left) and SHL (shift logical left). Both of these instructions
perform the same operation, and are interchangeable. They have three different formats:
sal destination
sal %cl, destination
sal shifter, destination
The first format shifts the destination value left one position, which is the equivalent of multiplying
the value by 2.
The second format shifts the destination value left by the number of times specified in the CL register.
The final version shifts the destination value left the number of times indicated by the shifter value.
In all formats, the destination operand can be an 8-, 16-, or 32-bit register or value in memory.
As always, the GNU assembler requires the usual one-character letter appended to the mnemonic to
indicate the size of the destination value.
The shift left instructions can be performed on both signed and unsigned integers. The bits emptied by
the shift are filled with zeroes. Any bits that are shifted out of the data size are first placed in the carry
flag, and then dropped in the next shift. Thus, if a value contains a 1 value in the most significant bit,
and is shifted left twice, the most significant bit will be dropped from the carry flag.
salx.s
salx.o
salx.exe # windows environment
Breakpoint 1, ?? () at users\rnz\desktop\salx.s:8
8 nop
(gdb) s
9 movl $10, %ebx
(gdb) s
10 sall %ebx
(gdb) s
11 movb $2, %cl
(gdb) s
12 sall %cl, %ebx
(gdb) s
13 sall $2, %ebx
(gdb) s
14 sall value1
(gdb) s
15 sall $2, value1
(gdb) s
16 movl $1, %eax
(gdb) info reg
eax 0x60ffcc 6356940
ecx 0x401002 4198402
edx 0x401000 4198400
ebx 0x140 320
esp 0x60ff74 0x60ff74
ebp 0x60ff80 0x60ff80
esi 0x401000 4198400
edi 0x401000 4198400
eip 0x40101c 0x40101c
eflags 0x212 [ AF IF ]
cs 0x23 35
ss 0x2b 43
ds 0x2b 43
es 0x2b 43
fs 0x53 83
gs 0x2b 43
(gdb) x &value1
0x402000 : 0x000000c8
(gdb) x/d &value1
0x402000 : 200
To follow along, the decimal value 10 is loaded into the EBX register.
00001010
The first SAL instruction shifts it one place (multiplying by 2, making 20).
00010100
The second SAL instruction shifts it two places (multiplying by
four, making 80),
01010000
and the third SAL instruction shifts it two more places (multiplying by four, making
320).
101000000
The value in the value1 location (25)
00011001
is shifted one place (making it 50),
00110010
and then shifted two more places (making 200).
11001000
Dividing by shifting
Dividing by shifting involves shifting the binary value to the right. However, as you shift an integer
value to the right, you must pay attention to the sign of the integer.
For unsigned integers, the bits to the left that are emptied can be filled with zeroes without any problems.
with signed integers, a negative number will be adversely affected by zero-filling
the leading bits.
To solve this problem there are two right-shift instructions. The SHR instruction clears the bits emptied
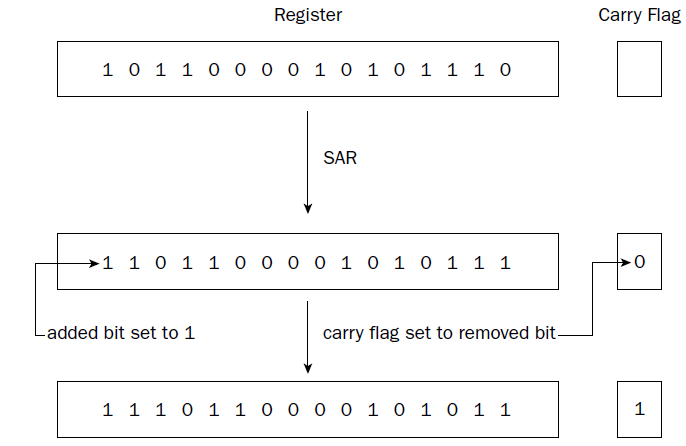
by the shift, which makes it useful only for shifting unsigned integers. The SAR instruction either clears
or sets the bits emptied by the shift, depending on the sign bit of the integer. For negative numbers, the
bits are set to 1, but for positive numbers, they are cleared to zero.
As with the left-shift instructions, the right-shift instructions shift bits out of the data element. Any bits
shifted out of the data element (the least significant bits) are first moved to the carry flag, and then
shifted out (lost).
Rotating bits
Close relatives to the shift instructions are the rotate instructions. The rotate instructions perform just
like the shift instructions, except the overflow bits are pushed back into the other end of the value
instead of being dropped. For example, a left rotate of a byte value takes the value in bit position 7
and places it in bit position 0, with each of the other bit positions shifted one place left.
The following table shows the various rotate instructions that can be used.

The last two instructions use the carry flag as an additional bit position, to allow 9-bit shifting. The formats
of the rotate instructions are the same as the shift instructions, providing three options for their use:
❑ A single operand that is shifted once in the indicated direction
❑ Two operands: The %cl register to indicate the number of times to rotate and the destination
operand
❑ Two operands: An immediate value to indicate the number of times to rotate and the destination
operand
Home Page

