PREFACE
The fundamental theorem of algebra describes the advantages of the utilzation of the complex numbers and their conjugates.
Let another kind of complex number be as:
 , where
, where 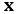 ,
, 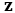 = horizontal axes ;
= horizontal axes ;  = vertical axis, and where
= vertical axis, and where 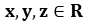
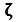 is not a Quaternion or other Cayley-Dickson construction.
is not a Quaternion or other Cayley-Dickson construction. 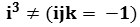
we note that
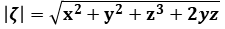
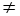
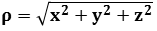
But, Let assume
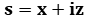 , a complex number that replaces
, a complex number that replaces 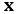 in a 2dimensional complex plane.
in a 2dimensional complex plane.
Then we assume that the modulus
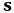 can rotate in the closed set
can rotate in the closed set 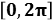 .
To use
.
To use 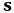 instead of
instead of 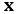 allows us to use three-dimensional space while maintaining the features of complex numbers.
So,
allows us to use three-dimensional space while maintaining the features of complex numbers.
So, 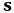 that intrinsically includes
that intrinsically includes 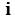 except the cases where the interaxles angle is
except the cases where the interaxles angle is 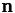
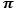 ,
,
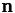 = integer, is a dependent variable and it is mobile in
all
= integer, is a dependent variable and it is mobile in
all 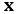 +
+ 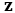 plane ,
by assigning appropriate values at
plane ,
by assigning appropriate values at 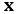 and
and 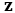 . The position of
. The position of 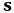 can range in
can range in 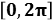 by the infinite factors of
by the infinite factors of 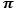
Then
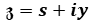
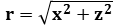
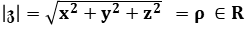
Moreover if
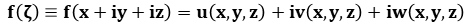
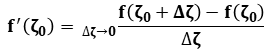
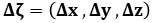 ,
, 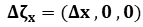 ,
, 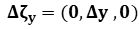 ,
, 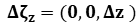
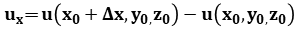
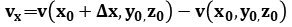

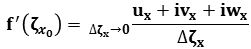
also by
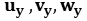 we have
we have 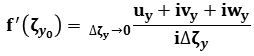 =
= 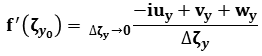
also by
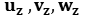 we have
we have 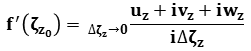 =
= 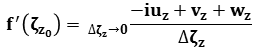
As
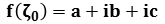 hence we have
hence we have
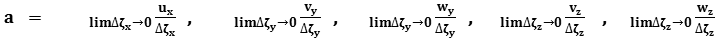
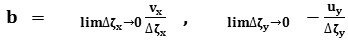
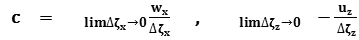
Holomorphy Conditions
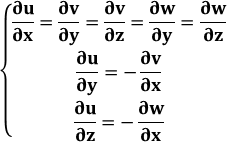
and deriving partially by
 on
on 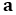 ,
, 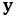 on
on 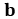 ,
,
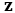 on
on 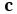 , we obtain
, we obtain
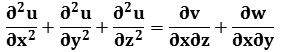
But if
in
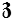 the Holomorphy conditions are the same in 2d-complex number:
the Holomorphy conditions are the same in 2d-complex number:
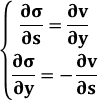
the Cauchy-Riemann equations in
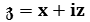 are
are 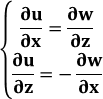 ,
,
deriving partially the first equation by
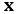 and the second equation by
and the second equation by 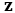 then
deriving partially the first equation by
then
deriving partially the first equation by 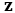 and the second equation by
and the second equation by 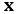 , we obtain
, we obtain 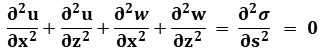
and about
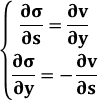 deriving partially the first equation by
deriving partially the first equation by 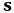 and the second equation by
and the second equation by 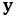 , we obtain
, we obtain 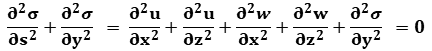 ,
,
instead, deriving partially the first equation by
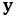 and the second equation by
and the second equation by 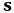 , we obtain
, we obtain 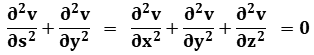
So we obtain the Laplacian on 3D on v-vector but not on u-vector neither w-vector . The laplacian equation is only on direction of axis
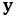 that links the north pole and south pole of the sphere
that links the north pole and south pole of the sphere  obtained by the Normed space consisting of vectors
obtained by the Normed space consisting of vectors 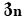 and
and 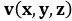 is the harmonic function of the laplacian equation on the v-vector
is the harmonic function of the laplacian equation on the v-vector
Trigonometric coordinates and Eulerian equations:
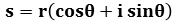

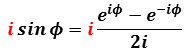
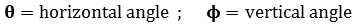
then
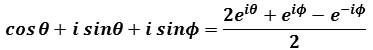
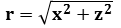 ,
, 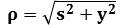
then

If
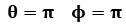 , then
, then 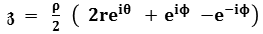 =
= 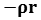 by Euler's identity
by Euler's identity
then also by De Moivre equations , with
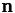 = integer
= integer
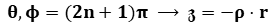
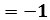 , (dot product)
, (dot product)
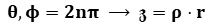
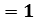 , (dot product)
, (dot product)
Since
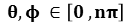
PI/4 approximately is 3.14159265358979/4 = 0.785398163397448
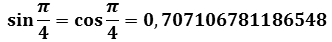
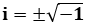 , considering
, considering 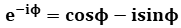 hence
hence 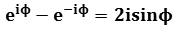
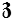
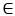

And if
 where
where 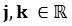
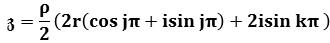
How wrong are we in calculating the position of the point
 and its vector?
we need to neutralize, as far as possible, the irrationality of
and its vector?
we need to neutralize, as far as possible, the irrationality of  to reduce the margin of error.
to reduce the margin of error.
eg: the angle have value
 , then assuming
, then assuming 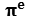 is not a transcendental number and
not even an irrational,
then, the calculation of the value of the angle would be more exact.
in this case, the argument to be used for the calculation of the angles should be
is not a transcendental number and
not even an irrational,
then, the calculation of the value of the angle would be more exact.
in this case, the argument to be used for the calculation of the angles should be  instead of
instead of
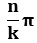 .
.
So in other case which
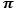 could be non-irrational,
eg
could be non-irrational,
eg 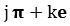 ,
, 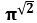 , the identification of the point position
, the identification of the point position  will be more precise.
will be more precise.